关注森林网

植言片语 | 植物中的斐波那契数列

什么是斐波那契数列

Fibonacci sequence

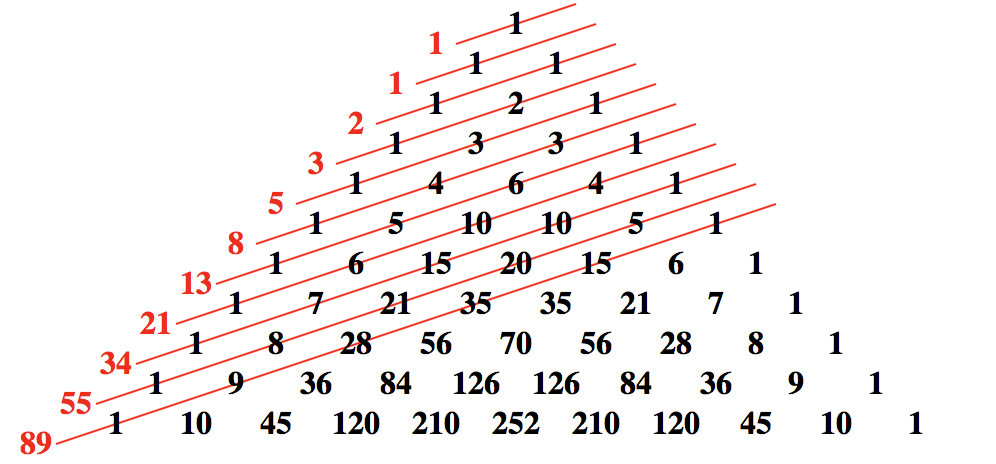
“1、1、2、3、5、8、13、21……”这组数列有着这样的规律：后项等于前两项之和。也就是说，1+1=2，1+2=3，2+3=5，3+5=8，5+8=13……以此类推可以继续算出后面的数字。此外，每个数字除以前边的数字，可以得到一个结果，数字越大，得到的结果越接近0.618，这个数字就是著名的黄金分割数。而这组数列被称为斐波那契数列。

不可思议的是，植物的生长竟然也遵循着这种黄金比例。

叶片

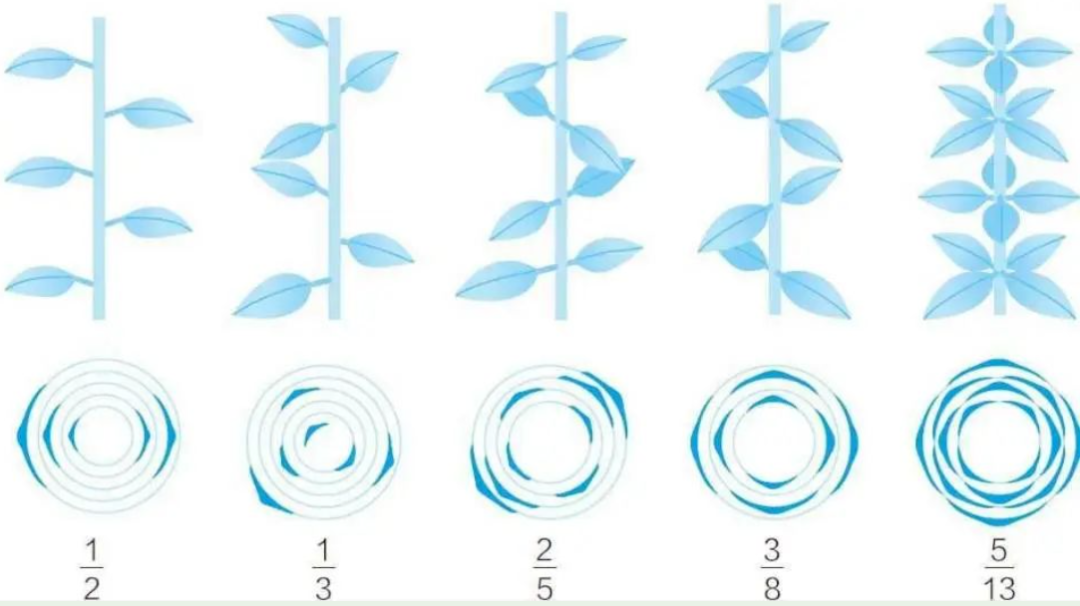
①植物叶片的生长位置，并不是毫无规律胡乱分布的。

为了使所有的叶子都能充分均匀地照射到阳光，植物会将叶子稍微错开排列。这种叶子的排列方法叫作叶序。而叶子要错开多少角度，则是由植物的种类决定的。比如说，有以360度的1/2，也就是180度角错开的。也有以360度的1/3，也就是120度角错开的。以这样角度错开的叶子，从下面往上数三片，就刚好转了一周回到了最初的位置。

此外，以360度的2/5，也就是144度角错开的情况也有。以这种角度错开的情况，我们从下面往上数，数到第五片叶子的时候，就转了两周回到了最初的位置。也就是说，我们只要数一下有几片叶子转了几周，就可以知道叶子错开的角度了。

除了上面提到的那些，还有以360度的3/8，也就是135度角错开的情况。

②1/2、1/3、2/5、3/8、5/13……实际上，这组分数的分子和分母，都是各自按照斐波那契数列排布的。植物的叶子按照斐波那契数列分布的这一规律，被称为兴柏-布朗定律。

用360度除以黄金比例1.618，可以得到222.5度。而从角度较小的那一侧看，是137.5度。这个角度，是遵循斐波那契数列规律的最精巧的角度。植物的叶子若以这样的数列规律排布，所有的叶片都不会重叠，可以充分地吸收阳光。此外，还可以使茎的强度更加均衡。话虽如此，因为无法做到以如此复杂的黄金比例来分布叶子，而以接近137.5度的、360度的2/5（144度）或是360度的3/8（135度）的角度来分布叶子的植物也有很多。

花瓣

让我们来看看花瓣的数量，百合花是3瓣，樱花是5瓣，大波斯菊是8瓣，金盏花是13瓣，玛格丽特花是21瓣，雏菊是34瓣，太阳花是55瓣。

3、5、8、13、21、34、55……让我们来观察一下，这组数据的规律是不是感觉在哪里见到过？

没错，实际上植物花瓣的数量，也遵循着我们在前文介绍过的斐波那契数列的规律。

植物花朵的部分，原本就是由叶子分化而成的。就像叶子为了实现最高效率，以斐波那契数列进行排布一样，花瓣为了实现最优最均衡的排布，也采用了斐波那契数列。

种子

许多植物的种子也按照斐波那契数列排列。

向日葵种子的排列成了两组镶嵌在一起的螺旋线，一组是顺时针方向盘绕，一组是逆时针方向盘绕。

虽然不同的品种中，种子的数量有所不同，但这两组螺旋线上的种子往往都是21和34、34和55、55和89、89和144这几组数字，每组数字都是斐波那契数列中相邻的两个数。

枝桠

树木生长过程中，由于新生的枝条往往需要一段休息时间，而后才能萌发新枝，所以，一株树苗在一段间隔，例如一年，以后才长出一条新枝；第二年新枝休息，老枝依旧萌发；此后，休息过一年的枝萌发，当年生的新枝则次年休息。

这样，一株树木各个年份的枝桠数，也构成斐波那契数列。这个规律，就是生物学上著名的“鲁德维格定律”。

https://mp.weixin.qq.com/s/ro4N-mhQpMGliSPeXMWFJw